'Skeleton Climbing': fast isosurfaces with fewer triangles Tim Poston , H.T. Nguyen , Pheng-Ann Heng and Tien-Tsin Wong , in Proceedings of Pacific Graphics'97, Seoul, Korea, October 1997, pp 117-126.

Abstract

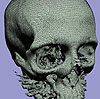
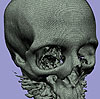
Skeleton Climbing is an algorithm that builds triangulated isosurfaces in 3D grid data, more economically than Marching Cubes, and without the time penalty of current mesh decimation algorithms. Building the surface from its intersections with grid edges (1-skeleton), then faces (2-skeleton), then cubes (3-skeleton), treats the data in a uniform way; this allows a 25% reduction in the number of triangles produced, while still creating a true separating surface at similar speed.

Download Paper

• Acrobat: sc.pdf (size: 2.64 MB)
  

Visual Comparison

The following table compares the statistical and visual results of the generated meshes.

Data Set	Marching Cubes	Skeleton Climbing w/o step 4	Skeleton Climbing with step 4
Knot
No of Triangles	13,968	13,968	10,464
Timing	1.81 sec	1.55 sec	1.61 sec
CT skull
No of Triangles	592,368	595,802	446,990
Timing	62.02 sec	63.38 sec	60.60 sec
Arteries
No of Triangles	263,438	265,536	195,588
Timing	55.82 sec	59.80 sec	63.15 sec
Mt. St Antonio
No of Triangles	268,252	268,368	201,686
Timing	113.77 sec	92.91 sec	96.33 sec